https://www.acmicpc.net/problem/23239
23239번: 당근 밭
입력은 표준입력을 사용한다. 첫 번째 줄에 마구간의 크기와 줄의 길이를 나타내는 3 개의 양의 정수 $w$, $h$, $L$ ($1 \le w, h, L \le 100,000$)가 주어진다.
www.acmicpc.net
1. 문제
💡 문제
무한히 넓은 당근 밭 가운데 x, y 축으로 수평인 직사각형 마구간이 있다. 그림 B.1 의 왼쪽 그림처럼 마구간의 왼쪽 아래 모서리 기둥에 말이 묶여 있고, 마구간의 네 모서리는 모두 격자점에 있다. 상하좌우로 인접한 두 격자점 사이의 간격은 1이다. 말을 묶은 줄의 길이는 'l'로 유한하다. 그리고 당근 밭의 모든 격자점마다 하나씩 당근이 심어져 있다. 그리고 말을 묶은 줄이 닿을 수 있는 거리 안에 심어진 당근은 말이 모두 먹을 수 있다고 가정한다.
만일 마구간의 크기가 11 × 6이고 묶은 줄의 길이가 9일때, 말이 먹을 수 있는 당근이 그림 B.1 의 오른쪽 그림에서 점으로 표시되어 있다. 단, 말과 말을 묶은 줄은 마굿간안으로는 들어갈 수 없으며 마굿간의 경계와 내부에는 당근이 심어져 있지 않다.
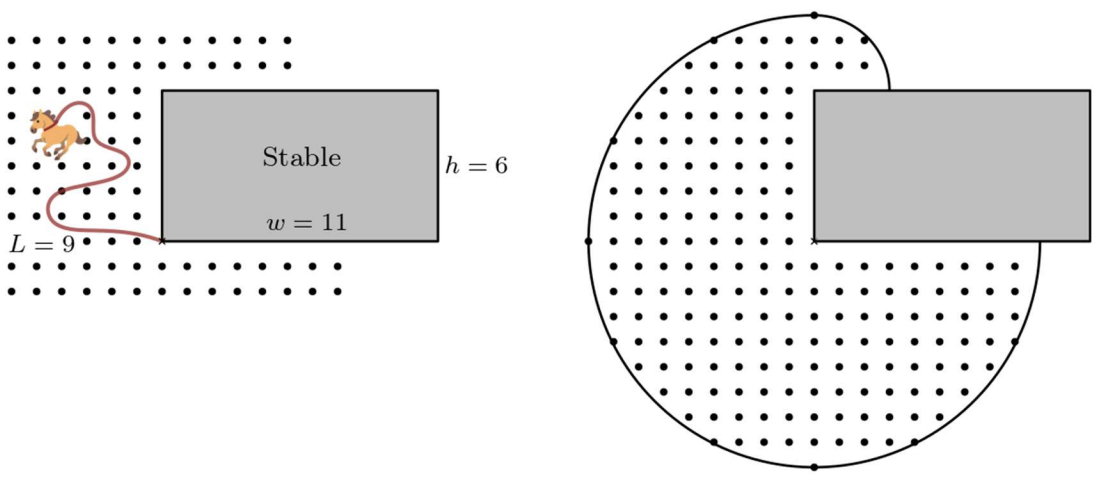
그림 B.1 (왼쪽) 마구간과 길이 9 인 줄에 묶인 말. (오른쪽) 말이 먹을 수 있는 모든 당근 (점).
마구간의 크기 'w × h'와 말을 묶은 줄의 길이 'L', 이렇게 3 개의 정수 'w', 'h', 'l' 이 주어졌을 때, 말이 먹을 수 있는 당근의 최대 개수를 구하는 프로그램을 작성하시오. 격자점과 말을 묶은 기둥과의 거리가 정확하게 'l'인 경우, 이 격자점의 당근은 말이 먹을 수 있음에 유의하자.
💡 입력
입력은 표준입력을 사용한다. 첫 번째 줄에 마구간의 크기와 줄의 길이를 나타내는 3 개의 양의 정수 'w', 'h', 'l' (1 ≤ w, h, L ≤ 100,000)가 주어진다.
💡 출력
출력은 표준출력을 사용한다. 주어진 조건에서 말이 먹을 수 있는 당근의 최대 개수를 첫 번째 줄에 정수로 출력한다.
2. 풀이
#include <stdio.h>
#include <math.h>
#define ll long long
ll h_Width, h_Height, h_Length, result = 0;
ll counting_Carrot(ll len){
ll carrot = 0;
ll temp = len - 1;
for(ll i = 1 ; i < len ; i++){
while(pow(i, 2) + pow(temp, 2) > pow(len, 2)) temp--;
carrot += temp;
}
return carrot;
}
ll remove_Carrot(){
ll carrot = 0;
ll temp = h_Length - h_Height - 1;
for (ll i = h_Height + 1 ; i < h_Length - h_Width ; i++){
while((pow(i - h_Height, 2) + pow(temp, 2) > pow(h_Length - h_Height, 2))
|| (pow(temp - h_Width, 2) + pow(i, 2) > pow(h_Length - h_Width, 2))) temp--;
carrot += (temp - h_Width);
}
return carrot;
}
int main(){
scanf("%lld %lld %lld", &h_Width, &h_Height, &h_Length);
result += counting_Carrot(h_Length) * 3 + h_Length * 2;
if (h_Length > h_Height) result += counting_Carrot(h_Length - h_Height) + h_Length - h_Height;
if (h_Length > h_Width) result += counting_Carrot(h_Length - h_Width) + h_Length - h_Width;
if ((h_Length - h_Height) > h_Width && (h_Length - h_Width) > h_Height) result -= remove_Carrot();
printf("%lld", result);
return 0;
}
3. 메모
진짜 너무 어려웠다. 수학만 만나면 뇌가 굳어버리는 것 같다. 처음에는 하나하나 구해가며 규칙을 찾으려고 했다 ㅋㅋ..
아래는 Height = 3, Width = 5, Length =15 일 때의 제 1 사분면 그림이다.

피타고라스 정리를 사용하여
1. 반지름이 'Length'인 원의 1 / 4 안의 당근 수 x 3 (2, 3, 4 사분면) + 1 / 4 원의 수직, 수평한 반지름 위에 존재하는 당근 수 x 2
2. 반지름이 'Length - Height'인 원의 1 / 4 안의 당근 수
3. 반지름이 'Length - Width'인 원의 1 / 4 안의 당근 수
4. 만일 2, 3번이 겹치는 부분이 있다면 겹치는 부분의 당근 수
1번부터 4번까지의 값을 구한 뒤, 1 + 2 + 3 - 4를 해주면 말이 먹을 수 있는 총 당근의 수가 나온다.
// 제 2, 3, 4 사분면 당근 수 구하기
ll counting_Carrot(ll len){ // counting_Carrot 함수에 매개변수로 줄 길이 (len) 전달
ll carrot = 0;
// 원의 수직 수평한 반지름 위에 놓인 당근 수는 따로 구해줄 것이기 때문에
// len - 1부터 시작
ll temp = len - 1;
for(ll i = 1 ; i < len ; i++){
// 삼각형의 대각선 길이가 반지름보다 크다면 temp -= 1
while(pow(i, 2) + pow(temp, 2) > pow(len, 2)) temp--;
// temp 값을 carrot에 더해준다
carrot += temp;
}
return carrot;
}
식이 복잡하게 보일 수 있지만 알고 보면 그렇지 않다. 다시 그림을 한 번 보자.

여기서 우리가 봐야 하는 부분은 검정 직삼각형이다. 아래 11칸, 오른쪽 6칸인 직삼각형. 먼저 피타고라스 정리를 사용해 직삼각형의 대각선 변 길이를 구해보자.

우리는 '12.5299 …' 라는 x 값을 얻을 수 있는데, 이 값은 'Length - Height'를 통해 얻은 값 12보다 크다. 그 말은 곧 곧 대각선 변과 수직인 변이 교차하는 지점의 좌표는 붉은 색 1 / 4 원 밖에 존재하고 있다는 것을 뜻한다.
for(ll i = 1 ; i < len ; i++){
while(pow(i, 2) + pow(temp, 2) > pow(len, 2)) temp--;
carrot += temp;
}위와 같은 방법으로 temp를 x 좌표로, i를 y 좌표로 하여 해당 좌표에서 대각선 길이가 1 / 4 원의 반지름보다 큰지 계속 비교한다.

제 2사분면, 제 3사분면, 제4사분면까지 위 코드대로 잘 따라왔다면, 이제 마굿간에 수직 수평인 반지름 위 당근까지 더해주면 노랑 3 / 4 원의 당근 수 세는 것은 끝이다.
result += counting_Carrot(h_Length) * 3 + h_Length * 2;
if (h_Length > h_Height) result += counting_Carrot(h_Length - h_Height) + h_Length - h_Height;
if (h_Length > h_Width) result += counting_Carrot(h_Length - h_Width) + h_Length - h_Width;
문제는 제 1사분면인데, 사실 앞서 사분면 당근 구했을 때와 똑같다. 붉은 1 / 4 원 당근에 푸른 1 / 4 원 당근을 더하고 녹색 부분을 제거해주면 된다.
ll remove_Carrot(){
ll carrot = 0;
ll temp = h_Length - h_Height - 1;
for (ll i = h_Height + 1 ; i < h_Length - h_Width ; i++){
while((pow(i - h_Height, 2) + pow(temp, 2) > pow(h_Length - h_Height, 2))
|| (pow(temp - h_Width, 2) + pow(i, 2) > pow(h_Length - h_Width, 2))) temp--;
carrot += (temp - h_Width);
}
return carrot;
}
int main(){
scanf("%lld %lld %lld", &h_Width, &h_Height, &h_Length);
result += counting_Carrot(h_Length) * 3 + h_Length * 2;
if (h_Length > h_Height) result += counting_Carrot(h_Length - h_Height) + h_Length - h_Height;
if (h_Length > h_Width) result += counting_Carrot(h_Length - h_Width) + h_Length - h_Width;
if ((h_Length - h_Height) > h_Width && (h_Length - h_Width) > h_Height) result -= remove_Carrot();
printf("%lld", result);
return 0;
}녹색 부분이 생기려면 'Length - Height > Width' 조건과 'Length - Width > Height' 조건을 모두 만족해야 한다. 두 조건을 만족할 때 , 결과값에서 remove_Carrot() 함수 리턴값을 빼주도록 하였다.
'프로그래밍 > 백준 알고리즘' 카테고리의 다른 글
| [C] 주사위 세 개 (백준 알고리즘 2480번) (0) | 2022.03.10 |
|---|---|
| [C] 오븐 시계 (백준 알고리즘 2525번) (0) | 2022.03.05 |
| [C] Fly me to the Alpha Centauri (0) | 2022.02.18 |
| [C] 1998년생인 내가 태국에서는 2541년생?! (0) | 2022.02.13 |
| [C] ??! (0) | 2022.02.11 |

